




Allied Link
History of the Cairo Tiling (from David Bailey)
From David Bailey's extensive site containing many deep analyses of interesting tessellations and their histories.
| Real world tiling | ||||||
| Appearance | Links |
Brief Remarks | Appearance | Links | Brief Remarks | |
|
|
Copenhagen |  |
Link | Bruges | ||
|
|
Savador Dali, playing with a classical deterministic tessellation involving squares and equilateral triangles. |
|
The definitive collection of regular (deterministic) tessellations: http://www.tilingsearch.org/ It features over 2000 different tiling patterns, many crowd-gathered from Islamic art, others from mathematical theory. | |||
 |
Link/Explanation Allied Link History of the Cairo Tiling (from David Bailey) |
Bev
Dunbar and Chrissy Monteleone's photo of "pentagon used to
decorate steps on a veranda in Earlwood, Sydney, Australia, dated about
the 1960s." From David Bailey's extensive site containing many deep analyses of interesting tessellations and their histories. |
||||
| Dailey's work with tiling (hosted at ello.co/ddailey and on cs.sru.edu/~ddailey) | ||||||
| Generally, in the majority of these, at least, a single tile (shape) is used, but its various orientations are all differently colored. So for example, the concave equilateral pentagon shown in the first row below, has 10 different orientations (each 36 i for 0 ≤ i < 360 degrees). I find this makes it easier to identify subtle differences between tessellations. | ||||||
| Appearance | Links |
Brief Remarks | Appearance | Links |
Brief Remarks | |
|
|
Link/explanation Allied link Allied link |
Concave equilateral
pentagon: an animated introduction Explore these, here, at your own pace (using scrollbars and zoom) |
|
Concave equilateral pentagon: animated gallery of options | ||
|
|
Link Allied link |
Experiments with clusters of the above concave equilateral pentagon. (It turns out there are 422 options for tetraominoes.) |
|
Link Allied link Allied link |
Fanciful arrangement of clusters of these. | |
|
|
Link |
|
Link | Concave Equilateral Heptagon. | ||
|
|
Link | One of three quadrilateral segments of an equilateral triangle. |
|
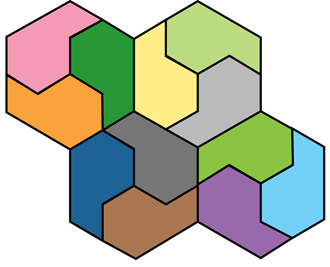
Link | Ways of partitioning hexagons into shapes which tile (ideally in ways other than the classical honeycomb/hexagonal tessellation). | |
|
|
Link | Quadrilateral half-hexagons. |
|
Link | Snowflake-like clusters of half-hexagons. (Pretty!) | |
|
|
Link | Showing how to tessellate in an outward spiral (avoiding all but a few hexagonal dominoes) and then replicating the resultant teardrop-pentagon from there. |
|
The clustered teardrop pentagon make some nice patterns, but I'm not sure if it can continue nondeterministically. | ||
|
|
Link | More experiments with a (larger) clustered spiral teardrop. |
|
Link | This particular cluster of half-hexagons forms an 18-sided polygon, which itself tessellates deterministically. | |
|
|
Link/explanation | Demonstrating how the L-triomino forms a "rep-tile" -- i.e., makes successively larger but similar (same shaped) versions of itself. |
 |
Link Explanation |
Triangle adjoining smaller
rhombus. 1/24th of an equilateral triangle. 1/12th of a hexagon. "reptiles" fractally. See also below (Another way of joining a large triangle with a smaller rhombus.) |
|
 |
Link | Double rhombuses aka sixths of a hexagon |  |
Link | V's and faultlines. To what extent can a periodic tiling be completely characterized by its partial faultlines? I don't know the answer. |
|
 |
explanation link | Gallery: Big and little triangles sharing an edge and a vertex to make a concave pentagon. |  |
explanation
link allied link |
Explorations: Big and little triangles sharing an edge and a vertex to make a concave pentagon. |
|
 |
Link Explanation |
Parallelograms: clusters of 3 x 4 and 4 x 3. Same tile as above but in curiously heterogeneous, though extensible arrangement. Note that it consists of differently oriented parallelograms, each composed of the same four basic orientations. |  |
Explanation Link |
Same as at left but with animated gradients (for fun) | |
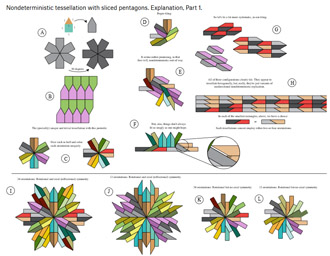 |
Link Explanation |
Sliced pentagons. Take an equilateral triangle and a square. Hook them together to make a pentagon. Then cut that in half. |  |
Link Explanation |
One of many tessellations involving the sliced pentagons seen at left. | |
 |
Link Explanation |
Castile and Leon come to Teotihuacan |  |
e-Link SVG Link |
S-shaped tile used radially. | |
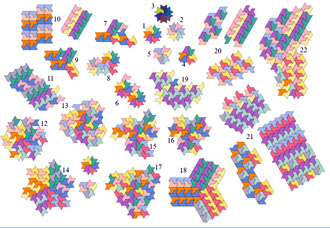 |
Link Explanation |
Heptagonal Hexatriominoes Close-up (1 - 5) Close-up (6 - 11) Close-up (12 - 18) Close-up (19 - 22) |
 |
Link Explanation |
Funky Mandala | |
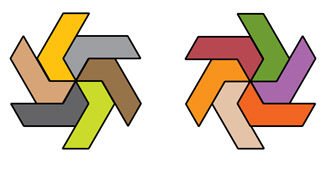 |
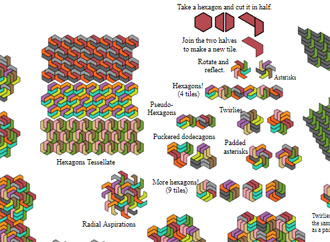
Link | Asterisks made of double half-hexagons. |  |
SVG
Link E-link |
Deconstructed asterisk using dominoes made of half-hexagons. | |
 |
Link Explanation |
Gallery of tilings made with double half-hexagons. |  |
Link Explanation |
Nonagonal Heptatriominoes: Seven triangles hooked together into a nonagon. | |
 |
Link Explanation |
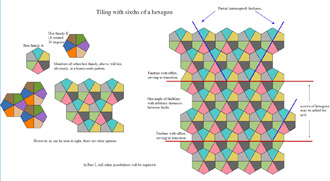
Tiling with thirds of a hexagon (Part I) |  |
Link Allied Link |
Tiling with thirds of a hexagon (Example) | |
 |
Link Explanation |
Tiling with thirds of a hexagon. Case study: transitions. | ||||
 |
Link other colors |
Heptagonal thirds of a hexagon. A slightly different shape than seen at left. It is also three of the double half hexagons seen above left (e.g., here). | ||||
 |
Explanation Link |
Tiling with sixths of a hexagon. Part 1. |  |
Link Explanation |
Tiling with sixths of a hexagon, Part 2. This shows that most of the ways that one might try to tessellate with this shape, simply don't work. | |
 |
Explanation Link |
Tiling with sixths of a hexagon. Part 3. |  |
Explanation Link |
Tiling with sixths of a hexagon. Part 4. I think I need to write a Part 5. | |
 |
Link | Reptiling with sixths of a hexagon, by making successively larger hexagons. | 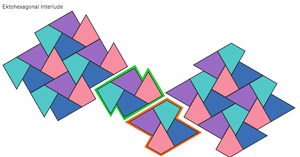 |
Explanation Link Explanatory link |
Nice tiling with ektohexagons. It's four-colored (meaning using four orientations) and faultless (meaning having no continued fault-lines -- unlike 'most' tesselations using this tile). | |
 |
Link Explanation |
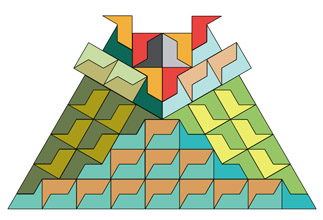
An idea based on the L-tetramino. I tried to replicate it along a base-line and to extend upward from there. It repeats horizontally but I am unsure if it can continue upward indefinitely.. | 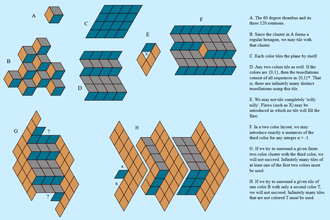 | Link and explanation | Tiling with the sixty degree rhombus. |
|
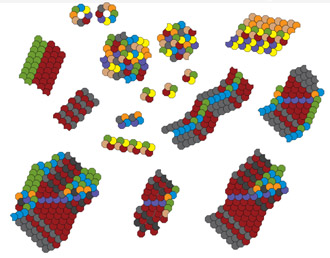 |
Link | Dented octagons |  |
Link | Octagonal crescents | |
 |
Link | A concave equilateral pentagon with interior angles of 60, 90, 60, 300 and 30. |  |
Link Explanation |
Guangdong-ese Cell Phone Towers. Tiling with V-shapes, made of six equilateral triangles. | |
 |
Explanation Link |
Same V-shapes as in above right. Originally, I wasn't sure if all the tiles had to be used as dominoes made into parallelograms or not. This shows that they don't.. | 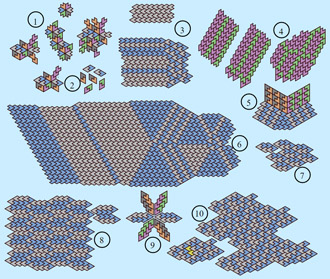 |
Explanation Link |
Gallery of tilings with the V-shape. | |
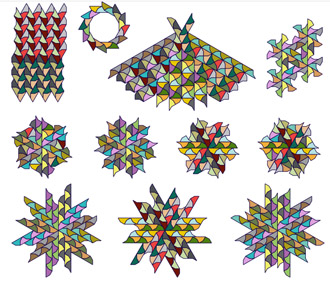 |
Explanation Link Link Link |
A fourth of a square with a bit of family history. |  |
Link Allied link |
Squares with equilateral triangles. | |
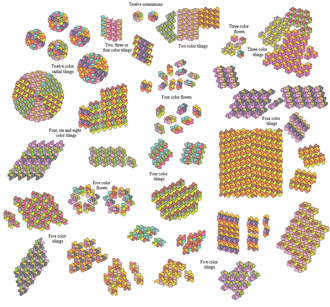 |
Link Explanation |
An irregular hexagon with a claw attached |  |
Link Explanation |
Two four-colored tilings that happen to coexist, using clawed hexagons | |
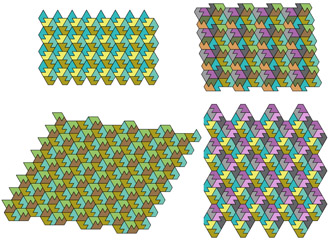 |
Link | Another way of joining a large triangle with a smaller rhombus. | 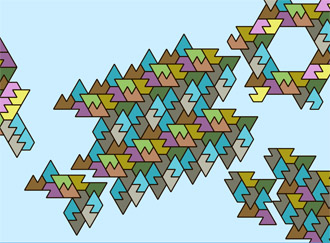 |
Link Explanation |
The same hexagon as at left (made with a big triangle and a little rhombus). | |
| Tessellation-like things (packings, knot tilings, paradoxes, etc) | ||||||
| Appearance | Links |
Brief Remarks | Appearance | Links | Brief Remarks | |
 |
Link Explanation |
Super-strong carbon mesh with quinary memory. (Simple nondeterministic paradoxical tessellation). See here for more on paradoxical tiling. |  |
Link | Deforming a square tessellation (using SVG animate) | |
|
|
Making moire-like patterns out of overlayed and animated squiggles. |
|
Link | Dynamic tessellations formed from shape-morphing animations. | ||
 |
Link Explanation Allied Link Allied Link Allied Link |
Positron emission tomography |  |
Animated
Explanation Scrollable Explanation Link/Explanation Allied Link |
Systematic enumeration of Knot-tiles | |
 |
Explanation Link |
Paradoxical tiling |  |
Link Explanation Allied link Allied link |
Heptadoilies | |
|
|
Link Explanation |
V-shaped thirds of a hexagon | ||||
|
|
|
|||||
| Animations of tessellations (already studied by others) including morphs. | ||||||
|
|
Hooking squares and equilateral triangles together, replicating and animating (just for fun) |  |
Link Allied Link |
Twirling the SVG pattern space of the (3,4,3,3,4) tessellation of squares and triangles. | ||
| Link Allied link |
More work with the (3,4,3,3,4) tiling, showing that it tiles nondeterministically. | Explanation | The (3,4,3,3,4) tiling is the first non-deterministic tiling I worked with, some forty years ago. I need to develop something deeper to show some of my investigations. | |||
|
|
Link | A fun concave decagon that hooks with itself. Also this demonstrates how to make a rectangular segment that can be used as an SVG <pattern> block to avoid having to replicate or re-<use>, hence allowing large-scale animations that are faster than the equivalent built of numerous vectors. |
|
Same as at left, but making the SVG <pattern> space visually obvious. | ||
|
|
Link | Morphing between two tessellations by expanding the borders (the grout) and celebrating them as full partners in tiling. |
|
Link | Bi-stable rotation of SVG pattern space | |
|
|
Link | Link Allied Link Allied Link |
Fun use of animated gradients in simple triangular tiling. | |||
|
|
Link |
|
Explanation | |||
 |
Link Allied Link Allied Link Allied Link |
Clock tiles |  |
Link Allied link |
Lacy veils of heptagons. | |