Chapter 12: Heaps
Data Structures and Algorithms in Java
CpSc 374
Max Heap Tree
- Complete binary tree
- For all subtrees, key(root) >= key(child)
- BSTs
- key(left child) < key(root)
- key(right child) > key(root)
- Heaps are Weakly Ordered
- Heap property less restrictive than BST
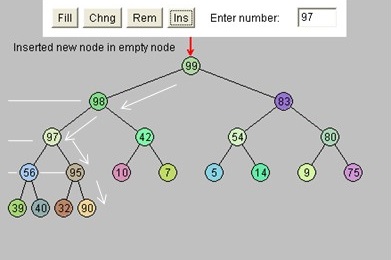
- Note that in the example, 95 is two levels below 83!
- all nodes along any path are in descending order.
- No "logical" traversals
- find() is O(N), so not typically supported
- Max Heap in Array
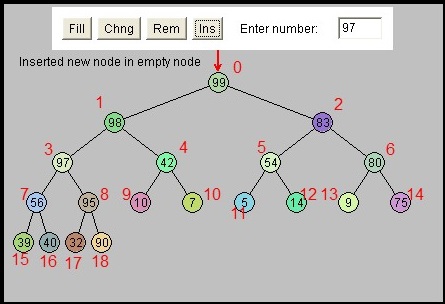

- Usually implemented in an array (no "holes"), so not "sparse" like BST
- Children located at myIndex*2+1 (left child) and myIndex*2+2 (right child)
For a Min Heap
- Smallest value is at root
- key(root) <= key(child)
- Ascending priority
Max Heaps are the Norm
- A descending-priority queue
- No loss of generality
- Heap is a data structure
class Heap {
private Node heapA[];
public void insert(Node nd)
{ ... }
public Node remove()
{ ... }
}
remove()
- If empty, retun null
- temp < root
- root < lastNode
- trim lastNode from tree
- trickleDown(root)
- return temp
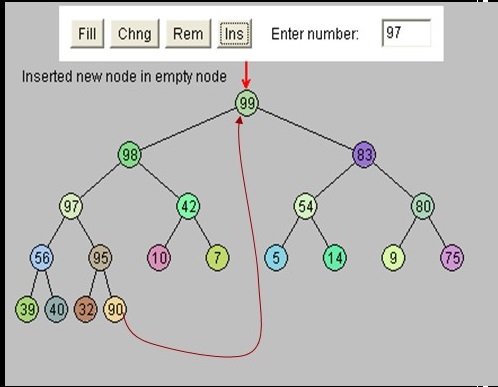
TrickleDown(myRoot)
while (myRoot < currentSize/2) // at least one child
promote < biggest(left, right) // temp to hold index
If (key(myRoot) < key(promote))
swap(myRoot, promote) // need to swap values in these locations
else break // found correct location
myRoot < promote // work on subtree
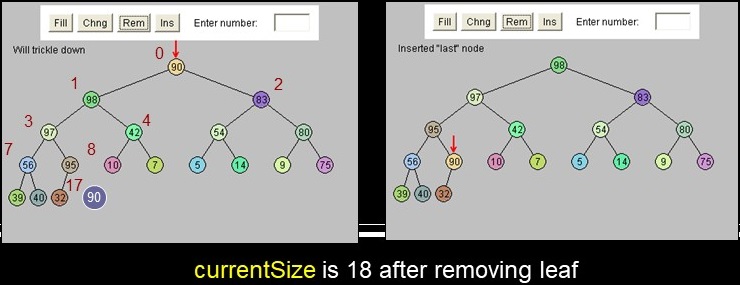 Remove & Trickle Down Example
Remove & Trickle Down Example
 Heap Code for remove
insert (key)
Heap Code for remove
insert (key)
- Place new node (nn) at last location in array (leftmost empty leaf location)
- trickleUp(index)
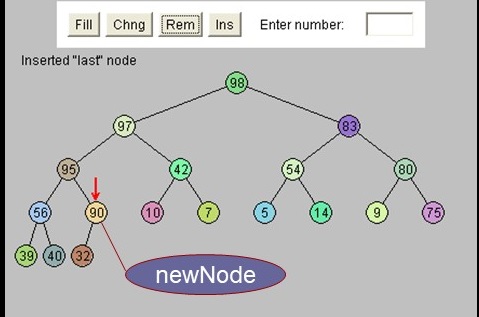
trickleUp(index)
while (index>0 && key(parent)< key(nn))
swap(parent, nn)
Update index and parent
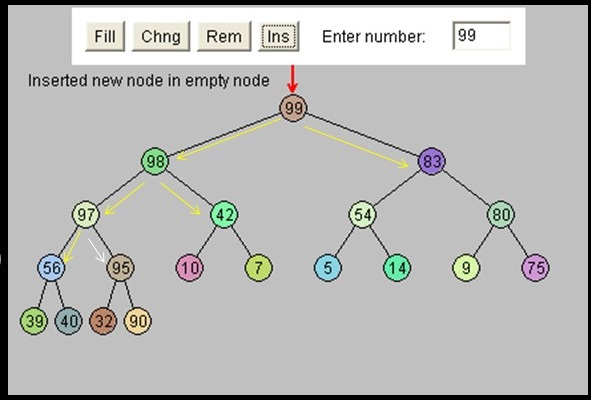
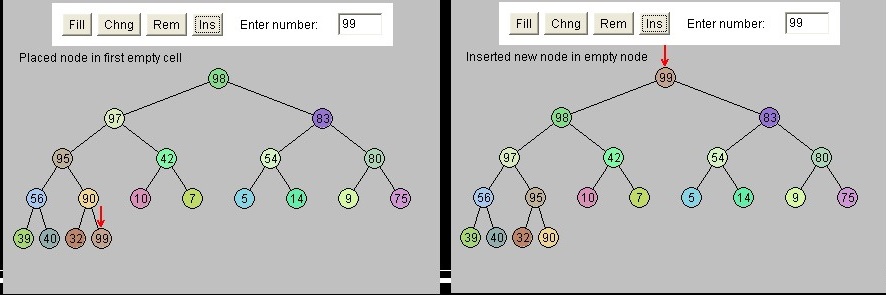 Insert & Trickle Up
Insert & Trickle Up
 Insert
Change a Priority
Insert
Change a Priority
- Determine that the priority of some item has to be changed
- Increase or decrease
- Need to find new "correct" location
- Also, need to find node to be changed: O(N)
- See
Heap Code for change method
Hidden cost of Change - O(N)
- Need to find(key) the node to be changed
- Tree structure implementation
- modified pre-order traversal
- only continue traversal to child if key is smaller then current root
- Array structure implementation
- just do a linear seach
Try find()
96 -
visit 7 of 19
41 -
visit 19 of 19
 Discussion
Discussion
- If array fills up...
- Use vector... or allocate new array & copy items
- Efficiency
- Insert & Remove ops bounded by (complete binary) tree depth, hence O(logN)
- Change op is O(N + logN)
- Using a (linked) tree structure - same efficiency
- Copy data from node to node to avoid changing links
Need parent pointers for trickleUp
Need access to "last node" (next location for insert)
Sorting... yet again
Selection sort (recall)
- On each pass over the data, find the largest key
- O(n) operation
- Put that one in its final location
- Repeat on smaller array (remaining elements)
- Hence, O(n2)
A heap gives us the largest value in O(log n)
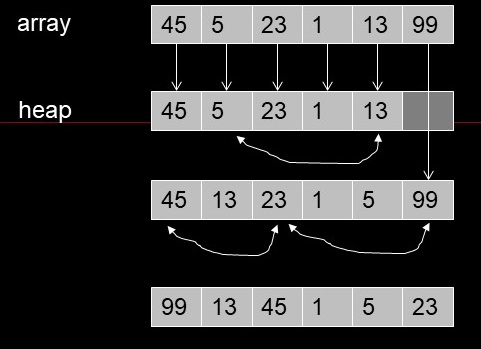
Heapsort
for(j=0;j<N;j++)
theHeap.insert(A[j]);
for(j=0;j<N;j++)
A[j] = theheap.remove();
- Efficiency
- N*logN + N*logN -->
- O(2N*logN) all cases
- Example
- Take element out of A...
- Use that location for the heap.
- There will always be exactly enough space for the heap.
Heap remove will always free the last array location...
- Put the removed element in that location.
Practice
WorkSheet
Josh's question got me thinking ...
Delete 111 and then 99 from this tree
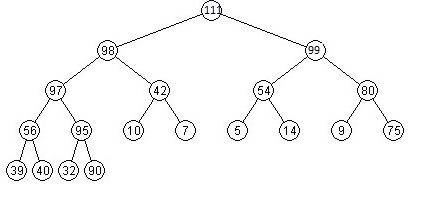











 Insert
Insert
 Discussion
Discussion

