- Insertion Sort
- In all cases, we look at each element: O(N)
- Average case: ~O(N/2)
- Have to move half of the already sorted elements
- Worst case: O(N)
- Have to move all of the already sorted elements
- Best case: O(1) (already sorted)
- Don't have to move anything
- Almost sorted, have to move a couple O(d)
- Insert Sort worst case, items are in reverse order
- Each element is very far from it's final location
- Requires max copy operations
- In best case, items are in order
- No element has to be moved
- We can approximate best case behavior if
- Only a couple items are out of position
- Or, each item is very near it's final location
Manipulating the Odds
- Can we arrange for items to be "very near" their final locations?
- Perhaps using a "pre-sort"
- Merge sort "pre-sorts" subarrays which are then merged...
- However, in the last step, half of the very small elements still end up N/2 positions away from final location...
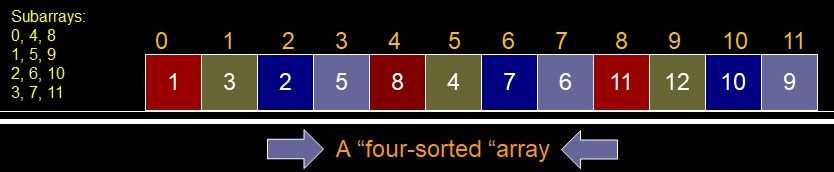
- Consider all odd indices an array and all evens an array??
- What if the subarray is "striped" throughout the array?
- Odds & evens are every second (every other) element
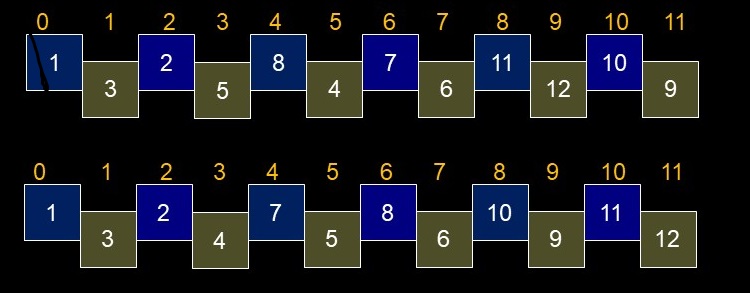
- Couldn't we use every fourth element?
- every fourth element treated as an element of a subarray => four subarrays
- Does this help?
- The smallest element has to be in location 0, 1, 2, or 3 since that is the smallest item in each subarray
- It would be "near" its final location
- Suppose it was in location 3 (not shown below)
- Next smallest is in 0, 1, 2, or 7
- What kind of average case behavior would you expect?
Shell Sort
- Start with gap0 = N
- Select a smaller gap to create subarrays
- (perhaps gapi+1 = gapi/2)
- Large enough that when sorted, elements jump a long way toward their "final" location
- Sort the sub-array using insertion sort
- Repeat while gap > 1
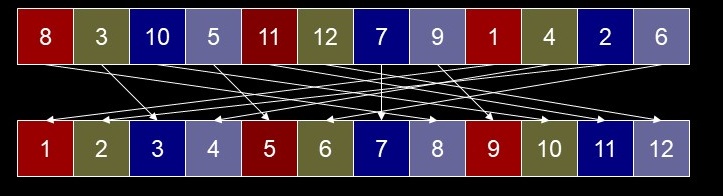
- Sequences for N = 12 elements:
- gap==6: (0,6) (1,7) (2,8) (3,9) (4,10) (5,11)
- gap==3: (0,3,6,9) (1,4,7,10) (2,5,8,11)
- gap==1: (0,1,2,3,4,5,6,7,8,9,10,11)
- At first, few elements are being sorted, but, elements are moving a long distance toward final destination
- As gap gets smaller, more elements are being sorted, elements move a moderate distance
- Finally, all elements are being sorted, but moving a small distance
- Last step is Insertion Sort on a nearly sorted array
Selecting the gap sequence
- Must end with gap == 1
- Experiments show N/2 is a poor choice
- Want gaps to be relatively prime
- (no common factors, except 1)
- Sometimes values do not "intermingle" well
- Degenerates to O(N2) for some data
- Though, still usually an improvement
- Unfortunately: No known "best" sequence
Knuth Sequence
- Before starting the sort
- Determine the largest h, h <= N/3
- From the sequence:
- h0 = 1
- hi = 3hi-1 + 1
Want h <=N/3 N h (h-1)/3 3 1 12 4 1 39 13 4 120 40 13 363 121 40 1092 384 121 3279 1093 365 - Use this hi as the initial gap0
- With each iteration, the next smaller gap is
- gapi = (gapi-1 - 1) / 3
- Author'sShell Sort Code

- First gap: h==4, Step 1
- Copy A[4] to temp
- temp == 11
- Find proper location by comparing to each element to the left & shifting if necessary
- There is only one element to the left
- 8 at A[0] which is smaller, so put temp in location A[4]
- Step 2
- Copy A[5] to temp
- temp == 12
- Find proper location by comparing to each element to the left & shifting if necessary
- There is only one element to the left
- 3 at A[1] which is smaller, so put temp in location A[5]
- Step 3
- Copy A[6] to temp
- temp == 7
- Find proper location by comparing to each element to the left & shifting if necessary
- There is only one element to the left
- 10 at A[2] which is larger, so shift it to the right
- Reached end, so put temp in location A[2]
- Step 4
- Copy A[7] to temp
- temp == 9
- Find proper location by comparing to each element to the left & shifting if necessary
- There is only one element to the left
- 5 at A[3] which is smaller, so put temp in location A[7]
- Step 5
- Copy A[8] to temp
- temp == 1
- Find proper location by comparing to each element to the left & shifting if necessary
- There are two elements to the left: A[4] & A[0]
- Both are larger and are shifted right
- Temp is placed at A[0]
- Step 6
- Copy A[9] to temp
- temp == 4
- Find proper location by comparing to each element to the left & shifting if necessary
- There are two elements to the left: A[5] & A[1]
- A[5] is larger and shifts right
- Temp is placed at A[5]
- Step 7
- Copy A[10] to temp
- temp == 2
- Find proper location by comparing to each element to the left & shifting if necessary
- There are two elements to the left: A[6] & A[2]
- Both are larger and shift right
- Temp is placed at A[2]
- Step 8
- Copy A[11] to temp
- temp == 6
- Find proper location by comparing to each element to the left & shifting if necessary
- There are two elements to the left: A[7] & A[3]
- A[7] is larger and shifts right
- Temp is placed at A[7]
- Step 9
- Reduce gap
- gap = (4 - 1) / 3 == 1
- Repeat => standard Insertion Sort
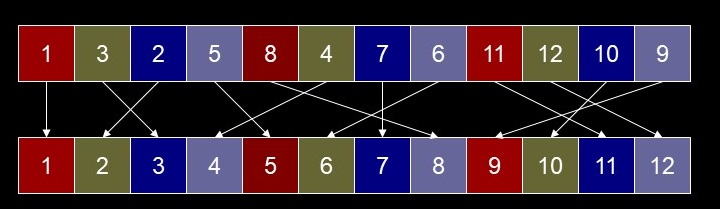
- On newly intermingled array
- Intermingling places items near final destination
- Distance from final loc for initial array
- Distance from final loc for new array
- Visualization of Shell Sort
- Time Efficiency
- Average & worst case (depends on gap)
- Estimates range from O(N3/2) to O(N7/6)
- Author recommends use Shell sort for up to a few thousand elements









| N | 10 | 100 | 1,000 | 10,000 |
|---|---|---|---|---|
| N2 | 100 | 10,000 | 1,000,000 | 100,000,000 |
| N3/2 | 32 | 1,000 | 32,000 | 1,000,000 |
| N7/6 | 14 | 215 | 3,200 | 46,000 |
| NlogN | 10 | 200 | 3,000 | 40,000 |
Partioning Data in an Array
- All elements to the left of the partition point are less than or equal to the pivot value
- All elements to the right of the partition point are greater than or equal to the pivot value
- Partition point - index at which above is true
- May not equally divide array Though we want to approximate this
- Not stable. Values equal to pivot will be swapped
- Author's Partition Code
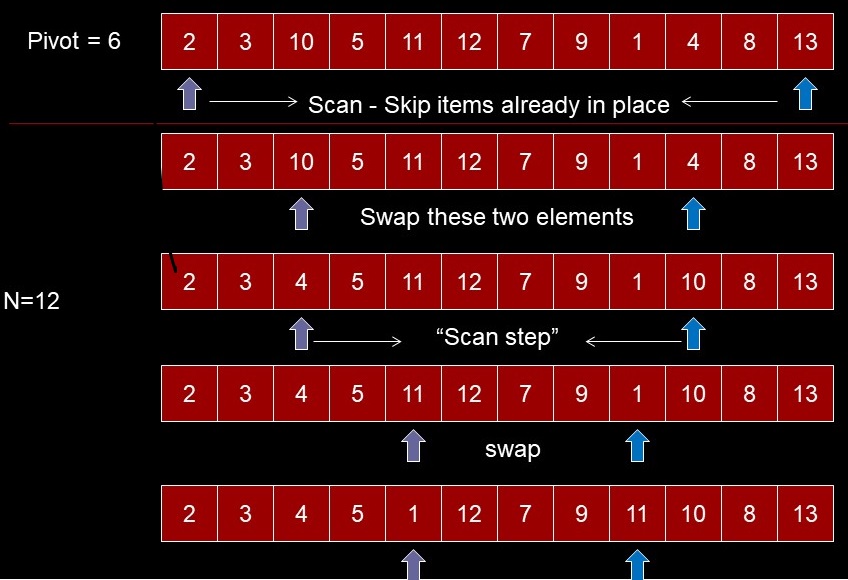
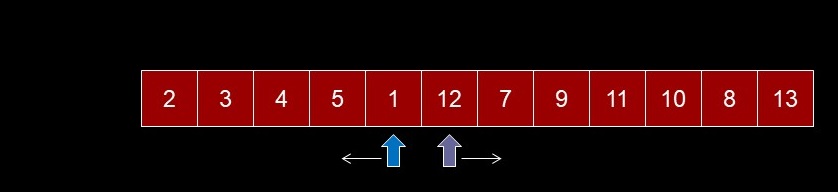
We are done since pointers cross over at this point or are at the same place
Partioned around pivot

- What if pivot value is in the array?
- Once found, it will always be swapped
- No more "skipping" on one side (alternates)
- But, it will end up in its final sorted position
- Use rightmost value as pivot, but exclude it from the partitioning...
- When done, array is still partitioned and we know final location for pivot value
- Modified Partion Code
public int partitionIt (int left, int right, long pivot)
{
int leftPtr = left - 1;
int rightPtr = right; /******/
while(true) {
// skip elems already in pos.
while(theArray[++leftPtr] < pivot) /********/
; // (nop)
while(rightPtr > 0 && /*****/
theArray[- -rightPtr] > pivot)
; // (nop)
if(leftPtr >= rightPtr)
break; // done
else
swap(leftPtr, rightPtr);
} // end while(true)
swap(leftPtr, right); // put in position
return leftPtr; //1st elem in upper
}
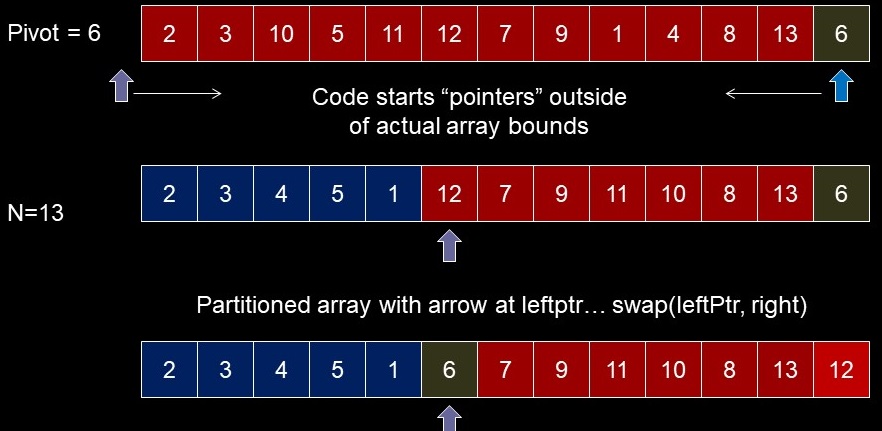 Top
Top
Quicksort Code (Hoare)
- Author's quickSort Code
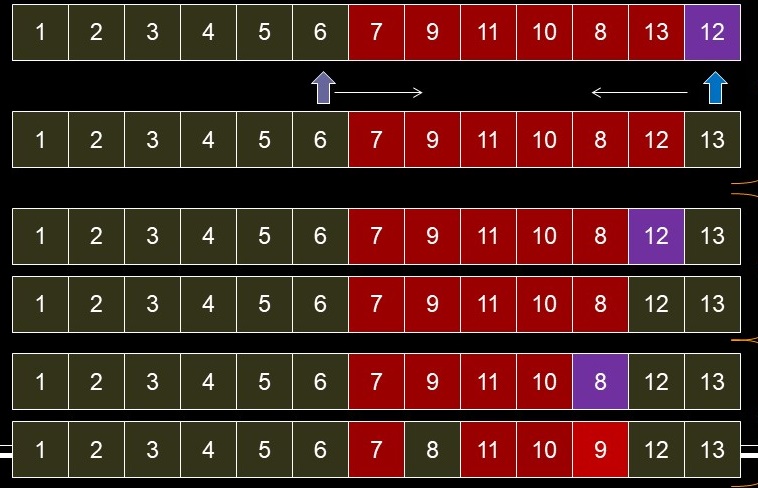
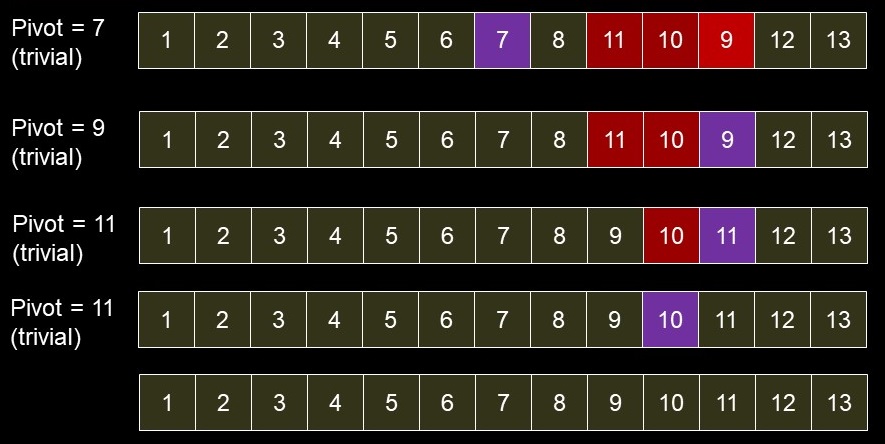
- For N of 13
- Recursively partition left sub-array
- Recursively partition right sub-array -- pivot is 12
- Recursively partition sub-arrays
- Using the rightmost element as the pivot:
- Ensures that the leftPtr cannot exceed array bounds
- Ensures finding the location of one element
- (which is swapped, then ignored>
- For inversely sorted data running time is O(N2)
- Every partition results in 1:N-1 elements
- Lot's of recursive calls - O(N)
- Want to use the median value as the pivot
- Giving approximately equal size partitions each time
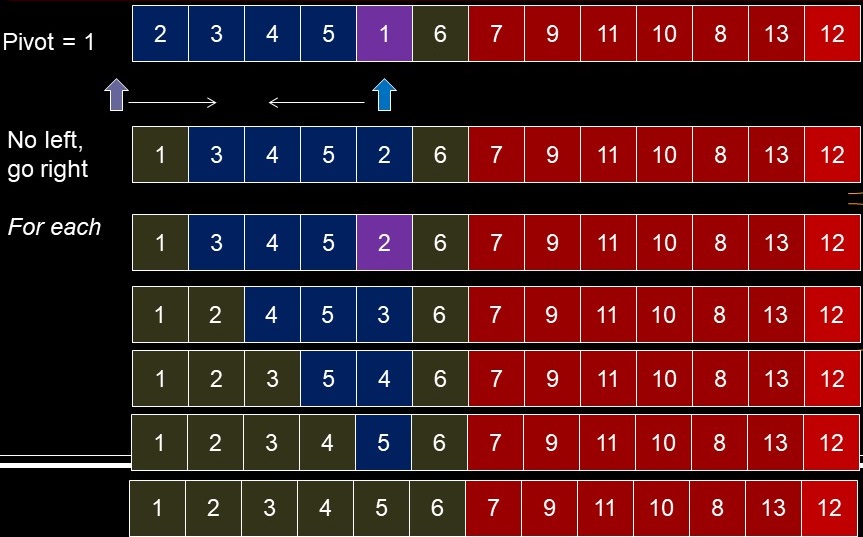
- Any value could be used for random data
- Use the median of the first, last and middle values (by position in array)
- If data is sorted, we get median of all
- Good odds of almost sorted
- Leave small value at left and large at right
- They act as sentinels, preventing out of bounds access
- Requires an initial "manual" sort of three elements
long median = medianOf3(left, right); int partition = partitionIt(left, right, median); recQuickSort(left, partition-1); recQuickSort(partition+1, right);
while( theArray[++leftPtr] < pivot ) /* nop */ ; while( theArray[--rightPtr] > pivot ) /* nop */ ;
- Requires partitions of at least three items
- Need to manually sort fewer items
- Fast - no more recursion
- Potentially 4 swaps, but still O(1)
- if (size <= 3)
public long medianOf3(int left, int right) { int center = (left+right)/2; // index if( theArray[left] > theArray[center] ) swap(left, center); if( theArray[left] > theArray[right] ) swap(left, right); if( theArray[center] > theArray[right] ) swap(center, right); swap(center, right-1); return theArray[right-1]; }
- Implies we don't want a manual sort
- Use Insertion sort
- Recommended for partition size of 9 or 10
- Recursive while size is greater, then switch
Radix Sort - uses information in keys
- Sort by Least significant (to most) digits
- Places in one of 10 buckets based on digit
- Read back in same order into array
- Repeat for next digit
- Use leading zero for smaller numbers
- Example with N=15, k=3, leading 0 digits shown
- First Digit

- Second Digit

- Third Digit

- Radix Discussion
- No comparisons
- Efficiency
- 2*N * (max number of digits in data)
- O(KN) worst case
- Uses more space than Quicksort
- LSD or MSD (not stable)
- Can be used for lexicographic ordering (strings) where K would refer to string length